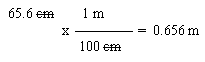
Bottom of page; return links and contact information
1. a & b. A meter is bigger, 1000 times bigger. The prefix milli means 1/1000, thus refers to a small amount. (Be sure to distinguish the prefixes milli and kilo.)
c. 1000 mm/1 m. Several variations of that are equivalent. For example, you might write what I gave but upside down. Or you might write 1000 in scientific notation. Or you might write something like 0.001 m/1 mm. All of these are fine.
Writing something like 1000 mm = 1 m is not correct. It is true, but it is not the answer to what was asked. The question asked for a conversion factor (CF), and this is an equation -- the equation from which the CF is derived.
2. a.
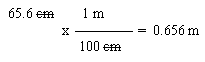
To do this, start with the given measurement, which is 65.6 cm. You want to convert to meters, so you need the relationship between the starting unit and the desired unit, between cm and m. In this case, you are given that relationship (but note that this is a basic relationship that you would be expected to know even by our first test). Write the relationship as a conversion factor, in such a way that the set-up looks useful. In this case, that means the cm goes on the bottom, so the cm "cancel", and the m goes on the top -- which is where you want it, in the final answer. Show which units "cancel", and make sure that the units left are what you want. Now, at last, do the arithmetic.
One way to show what you are thinking on a problem such as this is to explicitly write out the "given" and so forth, such as:
Given: 65.6 cm.
Wanted: meters.
Relationship(s): 100 cm = 1 m
Path: cm --> m (using 100 cm/1 m)Perhaps that is overkill for a one step problem such as this one. But perhaps it is more useful in a complex problem where you need to spend some time thinking out what the steps are.
The dimensional analysis set-up documents what you did. It shows what is given (the first term), what is wanted (the calculated result), and the steps in between. It is a sufficient explanation. Showing separately the given etc is an option that some people find helpful, sometimes. Use it as you find helpful.
The original measurement has 3 SF. The CF (conversion factor) is exact, as are all CF within the metric system. Thus the final answer should also have 3 SF, as shown.
b. A meter is bigger than a centimeter. Therefore, the measurement in meters should be a smaller number than the measurement in cm. That is, you need fewer m than you do cm, because each m is itself bigger. This is an example of a test for "reasonableness" of an answer. If you got 6560 m, that is unreasonable; go back and check your work. Always try to check your work for reasonableness.
3. 2.5 g/cm3. Density does not depend on the amount of material, but simply on the type. It is the ratio of the mass and the volume. (In this problem, mass is in grams and volume is in cm3; other units could be used.) So long as we are talking about the same material, that ratio is constant. That is the point; density is a property of the material, not of the amount. This is an important conceptual point. (We call such a property intensive. In contrast, mass does depend on amount; it is an extensive property.)
This question was taken from an article: R L Keiter et al, Density visualization. J Chem Educ 83:1629, 11/06. https://pubs.acs.org/doi/abs/10.1021/ed083p1629.
4. a. BMI = mass/height2 = 80 kg/(2.0 m)2 = 80 kg/(4.0 m2) = 20 kg/m2.
b. BMI = mass/height2 = 156 lb/(5'7")2 = 156 lb/(67")2. Now we need to convert this to the desired metric units.
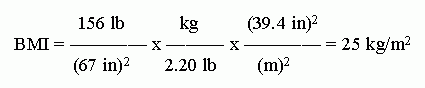
I have explicitly shown the units of BMI, though it is commonly given without units. However, it has units, and they are "understood". If you did not know the proper units for BMI, that illustrates the danger of omitting the units!
Be careful with the inch --> meter conversion. It is squared. That is, it is (inch --> meter)2, or inch2 --> meter2. That means the whole conversion factor (CF) is squared: the numeric part and the units part. If you have trouble seeing this, write out the simple CF twice -- which is what squaring means.
In doing this calculation, I used the conversion factors shown in the Intro Chem textbook I currently use. These CF have been rounded to 3 significant figures. If one uses more exact CF here, one would get BMI = 24. The calculated value is very near 24.4-24.5; thus the two-digit result is quite sensitive to the precise numbers, including CF, used. This is not really a problem. After all, most people would consider their height to be good to only one inch or so. BMI of 24 or 25 are not very different. That the common tables show a cutoff at 25 is arbitrary. It does not mean that you are "very healthy" at 24 and "very unhealthy" at 25. It is more an illustration of how rounding affects calculations.
Caution. Although BMI is something of practical interest, this is not the place to get into a detailed discussion of what it means. As an example of the complexity, it is quite likely that the significance of BMI varies among different groups of people, with other genetic or cultural differences. Thus saying that 'BMI = 25-26 is "borderline overweight".' is a guideline, one that has been determined for populations of "European" ancestry.
5. a. Density is mass/volume. Volume is proportional to the cube of the diameter. Thus the relative density is 200/(53) = 1.6.
For a sphere, V = (4/3) π r3 = (4/3) * π * (d3/8). But it is important to note that you do not need the formula for the volume of a sphere in order to do part a. All you need is the general idea that volume is proportional to the cube of the diameter -- something that should be apparent from the units of volume even if you do not remember much about calculating volume.
This is based on J S Kargel, Enceladus: Cosmic gymnast, volatile miniworld. Science 311:1389, 3/10/06. https://doi.org/10.1126/science.1124495. (This issue contains a feature section on Enceladus, with several articles.) The actual ratio of densities is about 1.3; the numbers given in the question are only approximate.
b.
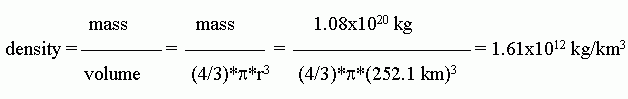
The units shown above are the natural units that fall out in this case. However, those units are not very helpful to most of us. 1.61x1012 kg/km3 = 1.61x106 g/m3 = 1.61 g/cm3.
Here is a set-up for that conversion:
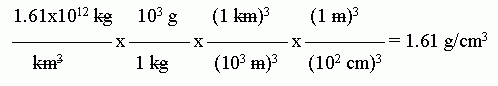
Be very careful with conversions involving units raised to a power. (This came up in the previous question.) The entire conversion factor must be raised to the power. This can be somewhat confusing to follow by the usual way we write the conversions. If you have trouble, it may be best to write, for example, (103 m)3 as (103)3 m3. Alternatively, you might write (103 m)3 as (103 m) * (103 m) * (103 m).
c. Density of water is 1.0 g/mL. It is well known that ice floats on water, so it must be less dense. Enceladus is considerably more dense than even liquid water. So, no, the density of the moon is much higher than expected from the suggestion that it is all ice.
6. 1.16x1037 (Round to 3 SF, like the "weaker" number.)
Please check with me if you have trouble with this question. If possible, do it in person, and bring the manual.
All of the issues raised here are dealt with on the calculator worksheet that is handed out in class, or available here on the Using your scientific calculator page.
The quiz Quiz list Intro Chem (X11) home page
Contact information Site home page
Last update: April 14, 2022