Bottom of page; return links and contact information
1. a. If you raise the T, the P will also rise (all else equal). P is proportional to T.
The new P is the old P, multiplied by the ratio of new and old T -- in Kelvins. So new P = 0.444 atm * (668 K/568 K) = 0.522 atm. Note that this is indeed more than the original pressure, as predicted.
b. Use the ideal gas law. Solve it for n: n = PV/RT:
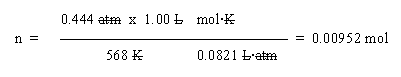
In that set-up, note that the T is given in K (always, in gas law problems). Also note that I have written R at the right side of the set up, just to help make it clearer. Watch the units carefully. The only unit left is mol, as desired.
c. At STP, 1 mol occupies 22.4 L. You have 1 L, which is approximately 1/20 of that, so we might expect 1/20 of a mol. But the P is approximately half of that for STP, and the T is approximately twice that of STP. Each of these deviations from STP means there is less gas in the container than expected -- by about 2x for each. Thus this quick estimate predicts about 1/80 mol -- in good agreement with the calculation, which says 1/100 mol.
Note that with this kind of estimation we are not trying to distinguish similar numbers such as 1/80 and 1/100. But if you had gotten 100 mol in part b (perhaps by setting up the calculation upside down), the estimate of 1/80 ~ 1/100 mol should lead you to re-check your work. You might even be suspicious if the calculation gave 0.1 mol -- almost 10 fold from the estimate.
d. Any ideal gas. You used the ideal gas law, which applies to any gas that meets its assumptions. As a practical matter, it is broadly applicable to gases, so long as they are not near condensing to a liquid.
2. Should look something like Fig 4.7 of Cracolice. More specifically, it should like Part a of that Fig, with the Hg level lower on the side with the container of gas -- by 20 mm. (We assume that the atmospheric pressure is 760 mm Hg.) The idea is that the pressure in the container is greater than the pressure in the atmosphere, so the end of the Hg column exposed to the container would be pushed down further.
3. a. We would need a column of water that weighs as much as the column of Hg (which weighs as much as the column of air). Since Hg is 13.6 times as dense as water, we would need 13.6 times more volume of water to get the same mass. 760 mm x 13.6 = 10,336 mm = 10.3 meters (which is >30 feet!).
b. As a practical matter, a water barometer would be too big. (But it would be more sensitive. It would be easier to detect small pressure changes with a water barometer than with a Hg barometer.)
The quiz Quiz list Intro Chem (X11) home page
Contact information Site home page
Last update: August 15, 2019