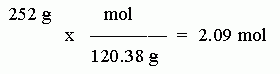
Bottom of page; return links and contact information
|
1. 2 AgNO3 (aq) + Na2S (aq) --> Ag2S (s) + 2 NaNO3 (aq)
Ion charges.
Phases.
2. Double replacement equations should balance rather easily. Many will balance with only 1 and 2 as balancing coefficients. In particular, the complexity of the balancing coefficients is about the same as the complexity of the ion subscripts in the chemicals. When you have trouble balancing one, it should be a clue that you might have one of the formulas wrong. So, if you didn't see the wrong formula, give it another try.
When you are ready, you can reveal the chemical whose formula is incorrect by putting your cursor over the link that follows. The chemical will be shown, after a momentary delay, in a balloon right near the link. Move your cursor over this link to reveal chemical with wrong formula. 3. The formula is Na2B4O7.10H2O. Molar mass = 2 Na (22.99) + 4 B (10.81) + 17 O (16.00) + 20 H (1.008). Total: 381.38 g/mol (or amu, but g/mol is more useful). (Number of decimal places is not important here, but be consistent.) |
4. Step 1: Determine the formula of the chemical. The magnesium ion is Mg2+. The sulfate ion is SO42-. Therefore, the neutral compound is MgSO4.
Step 2. Calculate the molar mass of the compound. (You know you will need this, because you are given mass, and asked to calculate moles.) Using all the digits shown on the class periodic table, this is 24.31 + 32.07 + 4*16.00 = 120.38 g/mol. Be sure you include the units.
Is it ok to give the units as amu/molecule (or amu per formula unit)? Well, it is certainly "correct" -- but it is also "useless", not appropriate for this problem.
Is it ok to give the molar mass as 120.4 g/mol? (That is, rounding to tenths.) Yes. The problem is given to 3 SF, so keeping four here should be no problem. However... why bother? To do this requires thinking ahead about how many SF you need. Seems to me it is easier to just keep all the digits during molar mass calculations, and round off at the end.
Is it ok to give the molar mass as 120 g/mol? (That is, rounding to integers.) Well, it is technically sort of ok. But it really is not a good idea. Every time you round off you introduce an uncertainty. These accumulate as you do more and more calculations. The less rounding you do before the final step, the better.
Is it ok to just use 16 for the atomic mass of oxygen? No. The periodic table gives the atomic mass of O as 16.00, with 4 SF. Using only 2 SF is throwing away two digits of information. If you did, you would only be able to report the formula mass for the compound to integers, and that is not so good, as discussed above. Avoid throwing away information. The purpose of this comment is to make you sensitive to noticing how many SF you have.
Step 3. Convert the given data, 252 grams, to moles, using the conversion factor you determined above. Round the result to 3 SF.
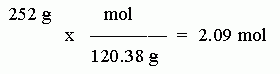
5. 2 KMnO4 (aq) + 8 HCl (aq) --> 3 Cl2 (g) + 2 MnO2 (s) + 4 H2O (l) + 2 KCl (aq)
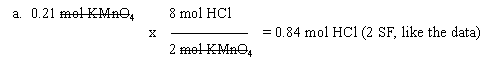
The conversion factor comes from the balanced equation. Balanced equations give you mole ratios of the chemicals in a reaction.
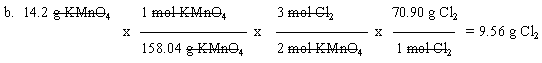
The final result has 3 SF, like the given data. Since you have 3 SF data, you must use molar masses with at least 3 SF, so they do not limit your result. (I encourage you to keep extra digits until the end, then round -- only -- the final answer.)
This is like part a, but with the additional complexity that you also need to convert between g and mol. Emphasize problems like part a at the start. Then move on to problems like part b. Students in high school or intro chem should be able to do both types of problem.
c. Cl2 is a gas; it will bubble off. All the other chemicals involved will stay in the container.
6. Given: 25 g water.
Wanted: dozens of molecules.
Path: grams --> moles of molecules --> molecules --> dozens of molecules
The path may or may not be obvious in advance. Think about it, try to find a path. Sometimes, the easy way is to start writing out the problem; see which conversion factors make the problem work. Look at your units; see what you need to do. Try it; trial and error. But this is why it is so important to write exactly what you mean in the set-up. The units are not decorations; they guide you to do the problem correctly. (And this is also why it is helpful to show what cancels; it helps you see what you really did. Make sure the units work.)
In this case, you should quickly recognize that, overall, the problem involves grams --> molecules, and therefore probably goes through moles. If you get this far, you can fill in the "details".
Start with the "given" data. (Starting with a CF is not a particularly good idea. For one thing, it's not logical. Further, you have a 50% chance of writing it upside down.)
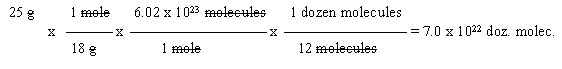
Note that the answer is rounded to two digits, like the given.
7. First, what is the chemical? Mercury (II) sulfide. HgS.
Now, calculate how many atoms are in one microgram (1 μg) of HgS.
Given: mass, in μg.
Wanted: number of atoms.
Path: μg --> g --> mol --> molecules --> atoms.
Molar mass of HgS: 233 g/mol.
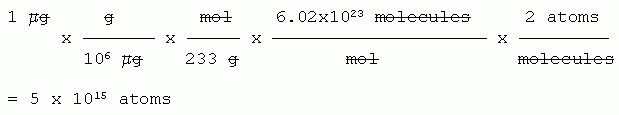
So, to address the question that was asked... Liebig suggested the answer should be something like 106, but we now know the answer is more like 1015. So he was low by a factor of about 109 -- a billion. Obviously, Liebig did not appreciate how very small atoms were.
Don't forget to answer the question! Merely doing the calculation shown above is not enough. The question was to compare Liebig's estimate with a modern calculation.
Significant figures? It should be clear from the question that you should not be worrying about them here. The question is a ball-park comparison. The question starts with "one" microgram of a substance (SF unclear), and refers to "millions" of molecules.
Is it important to include the term "2 atoms per molecule"? Well, logically it is very important. The question refers to the substance HgS, and asks about atoms. You should realize that 233 g/mol refers to "molecules" (or formula units) of HgS, each of which has two atoms. It would be sloppy thinking to skip this step. On the other hand, it would have no substantive impact on the conclusion reached for this particular question. Bottom line? I would take off if a student calculated molecules instead of atoms -- unless they made the point that it didn't matter much in this case. That is, I'll accept approximations that are stated, but not sloppy thinking.
This question is based on what Liebig reportedly said, as described in the book: J Buckingham, Chasing the Molecule, p 57.
8. a. Given: volume of gasoline.
Wanted: heat.
Think about what you know, and work out a general strategy, then fill in details. One thing you know is the heat per mole (stated in the question). That suggests:
volume (given) --> mass (using the density) --> moles (using the molar mass) --> heat (using the heat of combustion).
The only other difficulty is that the volume units are mixed. The given is in gallons, but the known conversion factors are in metric units. So, finally:
gal --> L --> mL --> g --> mol --> kJ.
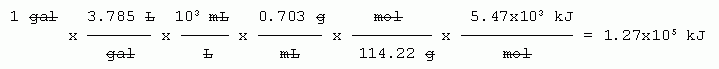
Balanced equation? Really don't need it. The only relationship we need about the reaction is the amount of heat given off per amount of octane, and that information is directly stated in the question.
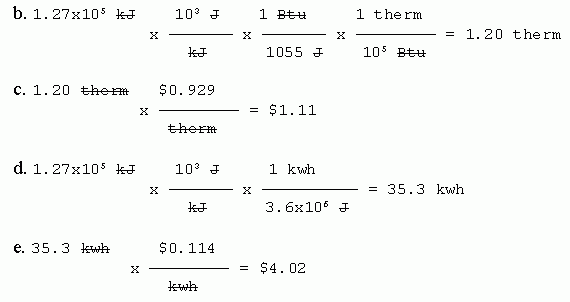
9. Ice water.
The quiz Quiz list Intro Chem (X11) home page
Contact information Site home page
Last update: July 15, 2019